Ripser.py — это компактный постоянный пакет гомологии для Python. Основанный на невероятно быстром пакете C++ Ripser в качестве основного вычислительного механизма, Ripser.py предоставляет интуитивно понятный интерфейс для вычисление когомологий персистентности разреженных и плотных наборов данных, визуализация диаграмм постоянства,вычисление фильтрации нижних звезд на изображениях и вычисление репрезентативных коцепей.
============================
В математике, особенно в теории гомологии и алгебраической топологии, когомологии — это общий термин для последовательности абелевых групп, обычно связанной с топологическим пространством, часто определяемым из коцепного комплекса. Когомологии можно рассматривать как метод присвоения пространству более богатых алгебраических инвариантов, чем гомологии. Некоторые версии когомологий возникают в результате дуализации построения гомологии. Другими словами, коцепи — это функции на группе цепей в теории гомологии.
Зародившись в топологии, эта идея стала господствующим методом в математике второй половины двадцатого века. От первоначального представления о гомологии как о методе построения алгебраических инвариантов топологических пространств диапазон приложений теорий гомологии и когомологий распространился на всю геометрию и алгебру. Терминология имеет тенденцию скрывать тот факт, что когомологии, контравариантная теория, более естественны, чем гомологии во многих приложениях. На базовом уровне это имеет отношение к функциям и обратным образам в геометрических ситуациях: для заданных пространств X и Y и некоторой функции F на Y для любого отображения f : X → Y композиция с f порождает функцию F ∘ f на X. У наиболее важных теорий когомологий есть продукт, чашечный продукт, который придает им кольцевую структуру. Из-за этой особенности когомологии обычно являются более сильным инвариантом, чем гомологии.
Вы можете найти исходный код на github по адресу Scikit-TDA/Ripser.py. Исходную библиотеку C++ см. в разделе Ripser/ripser.
(.env) boris@UbuntuLTS:~/RIPSER$ cat risperPlot3.py
from ripser import ripser
from persim import plot_diagrams
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
data = datasets.make_circles(n_samples=100)[0] + 5 * datasets.make_circles(n_samples=100)[0]
dgms = ripser(data)['dgms']
plot_diagrams(dgms, show=True)
"""
plot_diagrams(dgms, plot_only=[0], ax=plt.subplot(121))
plot_diagrams(dgms, plot_only=[1], ax=plt.subplot(122))
plot_diagrams(dgms, show=True)
"""
dgms = ripser(data, thresh=0.2)['dgms']
plot_diagrams(dgms, show=True)
dgms = ripser(data, thresh=1)['dgms']
plot_diagrams(dgms, show=True)
dgms = ripser(data, thresh=999)['dgms']
plot_diagrams(dgms, show=True)
(.env) boris@UbuntuLTS:~/RIPSER$ python3 risperPlot3.py
Ripser основан на когомологиях и возвращает репрезентативные коциклы для каждого генератора класса когомологий, возвращенного из алгоритма постоянных когомологий.
Напомним, что когомологии двойственны гомологиям, а кограничный оператор — это сопряженный оператор граничного оператора; то есть кограничный оператор принимает формы. Например, кограничный оператор переводит 0-формы (скалярные функции на вершинах) в 1-формы на векторном пространстве (функции на ориентированных ребрах) и переводит 1-формы в 2-формы (функции на ориентированных треугольниках). d-мерный коцикл — это -форма, кограница которой равна нулю. Как и в случае гомологии, двукратное применение кограничного оператора дает ноль; , поэтому образ находится в ядре , и мы можем взять частное, чтобы получить d-ю группу комологий. Конкретный класс эквивалентности -форм в этой группе, эквивалентный по модулю, называется классом когомологий. Алгоритм персистентных когомологий вычисляет набор генераторов класса когомологий, которые генерируют группу, и чьи рождения и смерти представлены на диаграмме персистентности (ПРИМЕЧАНИЕ: когомологическое рождение на самом деле является гомологической смертью, и наоборот, как мы увидим в нашем примере ниже, но мы все еще используем соглашение о рождении/смерти гомологии при построении диаграмм). Алгоритм персистентности возвращает репрезентативный коцикл для каждого класса генератора, который можно извлечь из рипсера и который мы сейчас исследуем на простом примере.
(.env) boris@UbuntuLTS:~/RIPSER$ pip install --force-reinstall matplotlib==3.4.2
============================================
UPDATE as of 7/11/2022
See Ripser.py 0.6.4 Representative Cocycles ( Matplotlib 3.6.2)
Version risperCohomology.py running with Matplotlib 3.6.2.
Code fixed for version 3.6.2.
============================================
(.env) boris@UbuntuLTS:~/RIPSER$ cat risperCohomology.py
import numpy as np
import matplotlib.pyplot as plt
from ripser import ripser
from persim import plot_diagrams
import tadasets
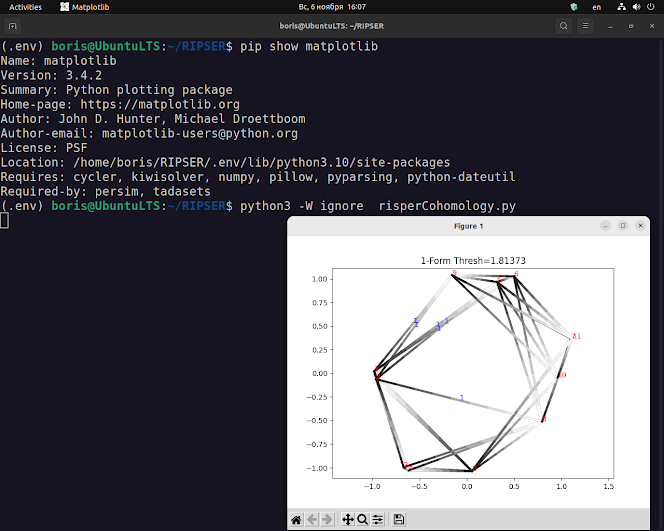
def drawLineColored(X, C):
for i in range(X.shape[0]-1):
plt.plot(X[i:i+2, 0], X[i:i+2, 1], c=C[i, :], lineWidth = 3)
def plotCocycle2D(D, X, cocycle, thresh):
"""
Given a 2D point cloud X, display a cocycle projected
onto edges under a given threshold "thresh"
"""
#Plot all edges under the threshold
N = X.shape[0]
t = np.linspace(0, 1, 10)
c = plt.get_cmap('Greys')
C = c(np.array(np.round(np.linspace(0, 255, len(t))), dtype=np.int32))
C = C[:, 0:3]
for i in range(N):
for j in range(N):
if D[i, j] <= thresh:
Y = np.zeros((len(t), 2))
Y[:, 0] = X[i, 0] + t*(X[j, 0] - X[i, 0])
Y[:, 1] = X[i, 1] + t*(X[j, 1] - X[i, 1])
drawLineColored(Y, C)
#Plot cocycle projected to edges under the chosen threshold
for k in range(cocycle.shape[0]):
[i, j, val] = cocycle[k, :]
if D[i, j] <= thresh:
[i, j] = [min(i, j), max(i, j)]
a = 0.5*(X[i, :] + X[j, :])
plt.text(a[0], a[1], '%g'%val, color='b')
#Plot vertex labels
for i in range(N):
plt.text(X[i, 0], X[i, 1], '%i'%i, color='r')
plt.axis('equal')
np.random.seed(9)
x = tadasets.dsphere(n=12, d=1, noise=0.1)
plt.scatter(x[:, 0], x[:, 1])
plt.axis('equal')
plt.show()
result = ripser(x, coeff=17, do_cocycles=True)
diagrams = result['dgms']
cocycles = result['cocycles']
D = result['dperm2all']
dgm1 = diagrams[1]
idx = np.argmax(dgm1[:, 1] - dgm1[:, 0])
plot_diagrams(diagrams, show = False)
plt.scatter(dgm1[idx, 0], dgm1[idx, 1], 20, 'k', 'x')
plt.title("Max 1D birth = %.3g, death = %.3g"%(dgm1[idx, 0], dgm1[idx, 1]))
plt.show()
cocycle = cocycles[1][idx]
thresh = dgm1[idx, 1] #Project cocycle onto edges less than or equal to death time
plotCocycle2D(D, x, cocycle, thresh)
plt.title("1-Form Thresh=%g"%thresh)
plt.show()
thresh = dgm1[idx, 1]-0.00001 #Project cocycle onto edges less slightly less than the death time
plotCocycle2D(D, x, cocycle, thresh)
plt.title("1-Form Thresh=%g"%thresh)
plt.show()
thresh = dgm1[idx, 0] #Project cocycle onto edges that have lengths less than or equal to the birth time
plotCocycle2D(D, x, cocycle, thresh)
plt.title("1-Form Thresh=%g"%thresh)
plt.show()
REFERENCES
1. https://ripser.scikit-tda.org/en/latest/notebooks/Basic%20Usage.html
2. https://ripser.scikit-tda.org/en/latest/notebooks/Representative%20Cocycles.html







No comments:
Post a Comment