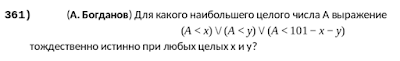Оригинальная формулировка задачи 361
Найти наибольшее А чтобы
(A < x1+2*x2+x3 ) v (A < 2*x1+x2+5*x3) v (A < 101-4*x1-4*x2-5*x3)
было истинно для всех х1,х2,х3 => 0
Допустим
(A < x1+2*x2+x3 ) v (A < 2*x1+x2+5*x3) =False
что равносильно
(x1+2*x2+x3 <=A )^(2*x1+x2+5*x3<= A) = True
Эквивалентная задача ЛП
(1) x1+2*x2+x3 <= A
(2) 2*x1+x2+5*x3 <= A
Определить максимум F(x1,x2,x3) =4*x1+4*x2+5*x3
Двойственная задача ЛП
y1+2*y2 >= 4
2*y1+y2 >= 4
y1+5*y2 >= 5
Определить минимум G(y1,y2) = A*y1+A*y2
============================================================
Теорема. (Первая основная теорема двойственности.) Если одна из двойственных задач имеет оптимальное решение, то двойственная ей задача также имеет оптимальное решение, причем экстремумы целевых функций равны.Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений.
===========================================================
Смотри также
https://1cov-edu.ru/lineynoe-programmirovanie/dvoystvennaya-zadacha/reshenie/
Строим область в плоскости соответствующую двойственной задаче
Решаем систему
(1) y1+2*y2= 4
(2) 2*y1+y2= 4
Минимум достигается в точке у1=4/3; y2=4/3
G(4/3,4/3) = A*(8/3)
A*(8/3)+A < 101
A*(11/3) < 101
A < 303/11
Откуда A(max)= 27
Подставим оптимальные значения у1 и у2 в 3-е уравнение
4/3+5*(4/3) = 24/3=8 > 5
По 2-ой теореме двойственности оптимальное х3 =0
Смотри https://1cov-edu.ru/lineynoe-programmirovanie/dvoystvennaya-zadacha/reshenie/
касаемо 2-ой теоремы двойственности , а также Пример 2.
Вторая теорема двойственности
*****************************************
Рассмотрим еще одну задачу
*****************************************
Найти наибольшее целое А чтобы
(A < x1+2*x2+4*x3 ) v (A < 2*x1+x2+11*x3) v (A < 101-4*x1-4*x2-20*x3)
было истинно для всех х1,х2,х3 => 0
Эквивалентная задача ЛП
(1) x1+2*x2+4*x3 <= AНайти наибольшее А чтобы
(A < x1+2*x2+x3 ) v (A < 2*x1+x2+5*x3) v (A < 101-4*x1-4*x2-5*x3)
было истинно для всех х1,х2,х3 => 0
Допустим
(A < x1+2*x2+x3 ) v (A < 2*x1+x2+5*x3) =False
что равносильно
(x1+2*x2+x3 <=A )^(2*x1+x2+5*x3<= A) = True
Эквивалентная задача ЛП
(1) x1+2*x2+x3 <= A
(2) 2*x1+x2+5*x3 <= A
Определить максимум F(x1,x2,x3) =4*x1+4*x2+5*x3
Двойственная задача ЛП
y1+2*y2 >= 4
2*y1+y2 >= 4
y1+5*y2 >= 5
Определить минимум G(y1,y2) = A*y1+A*y2
============================================================
Теорема. (Первая основная теорема двойственности.) Если одна из двойственных задач имеет оптимальное решение, то двойственная ей задача также имеет оптимальное решение, причем экстремумы целевых функций равны.Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений.
===========================================================
Смотри также
https://1cov-edu.ru/lineynoe-programmirovanie/dvoystvennaya-zadacha/reshenie/
Строим область в плоскости соответствующую двойственной задаче
(1) y1+2*y2= 4
(2) 2*y1+y2= 4
Минимум достигается в точке у1=4/3; y2=4/3
G(4/3,4/3) = A*(8/3)
A*(8/3)+A < 101
A*(11/3) < 101
A < 303/11
Откуда A(max)= 27
Подставим оптимальные значения у1 и у2 в 3-е уравнение
4/3+5*(4/3) = 24/3=8 > 5
По 2-ой теореме двойственности оптимальное х3 =0
Смотри https://1cov-edu.ru/lineynoe-programmirovanie/dvoystvennaya-zadacha/reshenie/
касаемо 2-ой теоремы двойственности , а также Пример 2.
Вторая теорема двойственности
*****************************************
Рассмотрим еще одну задачу
*****************************************
Найти наибольшее целое А чтобы
(A < x1+2*x2+4*x3 ) v (A < 2*x1+x2+11*x3) v (A < 101-4*x1-4*x2-20*x3)
было истинно для всех х1,х2,х3 => 0
Эквивалентная задача ЛП
(2) 2*x1+x2+11*x3 <= A
Определить максимум F(x1,x2,x3) =4*x1+4*x2+20*x3
Двойственная задача ЛП
y1+2*y2 => 4
2*y1+y2 => 4
4*y1+11*y2 => 20
Определить минимум G(y1,y2) = A*y1+A*y2
Строим область в плоскости соответствующую двойственной задаче
Решаем систему
(1) y1+2*y2= 4
(2) 2*y1+y2= 4
Минимум достигается в точке у1=4/3; y2=4/3
G(4/3,4/3) = A*(8/3)
A*(8/3)+A < 101
A*(11/3) < 101
A < 303/11
Откуда A(max)= 27
Подставим оптимальные значения у1 и у2 в 3-е уравнение
4*(4/3)+11*(4/3) = 60/3=20=20
Следовательно, оптимальное х3 для этой задачи не обязано вырождаться в 0
****************************************************************************
Элементарный подход к решению задач клонов
361 ЕГЭ Информатика 2019 для пространства R^3
****************************************************************************
Найти максимальное целое А такое что
(A < 2x1+4x2+x3)v( A < x1+7x2+4x3)v(A < 101 - (6x1+28x2+8x3))
было тождественно истинно для всех х1,х2,х3 => 0
Эквивалентная задача ЛП
Область Допустимых Решений
(1) 2*x1+4*x2+x3 <=A
(2) x1+7*x2+4*x3 <=A
(3) х1,х2,х3 => 0
Определить максимум F(x1,x2,x3) =6x1+28x2+8x3
Элеметарное решение,использующее параметризованное
уравнение прямой , лежащей в пересечении плоскостей
- линия PQ на рисунке ниже
(1) 2*x1+4*x2+x3 = A
(2) x1+7*x2+4*x3 = A
Положим х3 = t
2*x1 + 4*x2 + t = A
x1 + 7*x2 + 4*t = A | *2
10*x2 = A-7*t
x2 =(1/10)*(A-7*t)
2*x1 + (2/5)*(A-7*t) + t = A
10*x1 + 2*(A-7t) + 5*t = 5A
10*x1 - 9*t = 3A
x1 = (3/10)*(A+3*t)
Найдем точку пересечение прямой
x1 = (3/10)*(A+3*t)
x2 = (1/10)*(A-7*t)
х3 = t
с плоскостью уровня 6x1+28x2+8x3 = С,имеющую максимально
возможное С при заданном параметре А, меняя значение переменной "t".
Для этого подставим х1,х2,х3 как функции от "t"
в уравнение плоскости уровня (С) и уменьшая
текущий параметр "t" увеличиваем С как функцию параметра А
(9/5)*(A+3*t) + (14/5)*(A-7*t) + 8*t = C
(23/5)*A + ((27-98+40)/5)*t = C
(23/5)*A - (31/5)*t = C
C(max) = (23/5)*A ; t = 0
Проверим , что точки (А/2,0,0),(0,A/7,0),(0,0,А/4),((3/7)A,0,(1/7)A)
находятся в полупространстве 6*х1+28*х2+8*х3 <(23/5)*A,
a в точке ((3/10)A,(1/10)A,0) имеет место равенство
6*х1+28*х2+8*х3 =(23/5)*A
(23/5)*A < 101 -A
(28/5)*A < 101
A < (505/28)
Откуда A(max)=18
Двойственная задача ЛП
(1) 2*y1+y2 =>6
(2) 4*y1+7*y2 =>28
(3) y1+4*y2 => 8
(4) y1,y2 => 0
Определить минимум G(y1,y2) =A*y1+A*y2
По-существу, все действия, описанные выше немедленно вытекают из 2-ой теоремы двойственности. Смотри
https://mapping-metod.blogspot.com/2019/04/361-ege18doc-3.html