Задача 18 ВКонтакте от 06/07/17

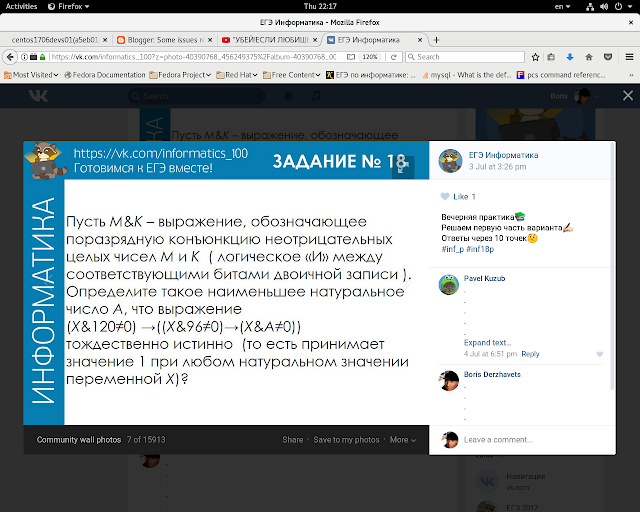
   (x&120 != 0) => (┐(x&96 !=0) v (x&A !=0))
   ┐(x&120 != 0) v (┐(x&96 !=0) v (x&A !=0))
   ( ┐(x&120 != 0) v (┐(x&96 !=0)) v (x&A !=0)

  Analyze when  ( ┐(x&120 != 0) v (┐(x&96 !=0)) is False

  ┐(x&120 != 0) = False (1)
  ┐(x&96 !=0)   =  False (2)

   (x&120 != 0) = True
   (x&96 !=0)   =  True


   120 = 1111000 ( binary)
   96   = 1100000  (binary)

Let's say that x is called  jeopardizing if it makes
    ┐(x&120 != 0)   =  False (1)
    ┐(x&96!  =  0)   =  False  (2)


Thus

   1   1   1  1 0  0 0  = 120 (decimal)
x
   x7x6x5x4x3x2x1

shouldn't be 0

   1   1   0  0  0 0  0   =96 (decimal)
x
   x7x6x5x4x3x2x1

shouldn't  be 0

   Consider jeopardizing bits in 120 and 96

   So for first equation { x7,x6,x5,x4 } should have  at least one bit equal 1
        for second equation { x7,x6 } should have at least one bit equal 1
 
  The minimal A (96) should have x7=1 x6=1 due to jeopardizing
  x might have 1 on position x7 or x6 and another 0.   
  First condition would also be satisfied when 

  x=11***** (binary) where "*' may be 1 or 0.
    or
  x=01*****(binary)
   or
 x=10***** (binary)

 if x7 and x6 are both equal 0 then

   1   1   0  0  0 0  0   =96 (decimal)
x
   x7x6x5x4x3x2x1

would  be equal 0. What breaks condition (2)

  So we must defend by 1 any of two  first  positions  in number A 
  and filed the rest positions with 0 to minimize A.

  Thus    A= 1100000 (binary) = 96 (decimal)

  I believe we are done with task 18

*************************
Another task
*************************

    (x&120 != 0) => ((x&96 =0) => (x&A !=0))

Proceed as follows :-

    (x&120 != 0) => (┐(x&96 =0) v (x&A !=0))
   ┐(x&120 != 0) v (┐(x&96 =0) v (x&A !=0))
   ( ┐(x&120 != 0) v (┐(x&96 =0)) v (x&A !=0)

  Analyze when  ( ┐(x&120 != 0) v (┐(x&96=0)) is False
  ┐(x&120 != 0) = False (1)
  ┐(x&96 =0)   =  False (2)

   (x&120 != 0) = True
   (x&96 =0)   =  True


   120 = 1111000 ( binary)
   96   = 1100000  (binary)

Let's say that x is called  jeopardizing if it makes
    ┐(x&120 != 0)   =  False (1)
    ┐(x&96  =   0)   =  False (2)

Thus

   1   1   1  1 0  0 0  =  120 (decimal)
x
   x7x6x5x4x3x2x1

shouldn't be 0

   1   1  0  0  0 0  0   = 96 (decimal)
x
   x7x6x5x4x3x2x1

should  be 0


   Thus  for any of  jeopardizing x we should have (x&A != 0), otherwise we don't
  have any problem because at least one of (1) or (2) is True


      Consider jeopardizing bits in 120 and 96

   So for first equation { x7,x6,x5,x4 } should have  at least one bit equal 1
        for second equation { x7,x6 } should have x7=0 and x6=0

  So A=0011000 = 11000 (binary) = 24 (decimal)